
A/B Testing and how to implement it in Python
Author: Fallah
A/B Testing, also known as split testing, is a method of comparing two or more versions of a variable (web page, mobile app, newsletters etc.) against each other to determine which one performs better.
A/B testing can be used to…
- evaluate which form of website design increases user interactions with your website, such as purchases, sign-ups, etc…
- determine which components of your products/services drive value.
- identify the impact of a new app rollout on your app’s average revenue.

Testing one page against one or more variations that contain one major difference in an element:
Control: The current state of your page
Treatment(s): The variant(s) that you want to test
- Let’s consider the following scenario:
NuFace provides anti-aging skincare products directly to its customers. They found that although people were interested in their products, not many were completing their
purchases. And this wasn’t in line with NuFace’s goals to grow their online process and improve their conversion rate from 12% to 14%.
Hypothesis: If we display a price comparison with their competitors, there will be more sales and order completions.
- For our test we randomly subset the users and show one set the control group (old design) and one the treatment group (new design).
- we are interested in tracking the conversion rates of each group to see which is better.
- The hypothesis that they came up with was that they suspected including testimonials on the page would increase visitor trust and lead to more conversions.
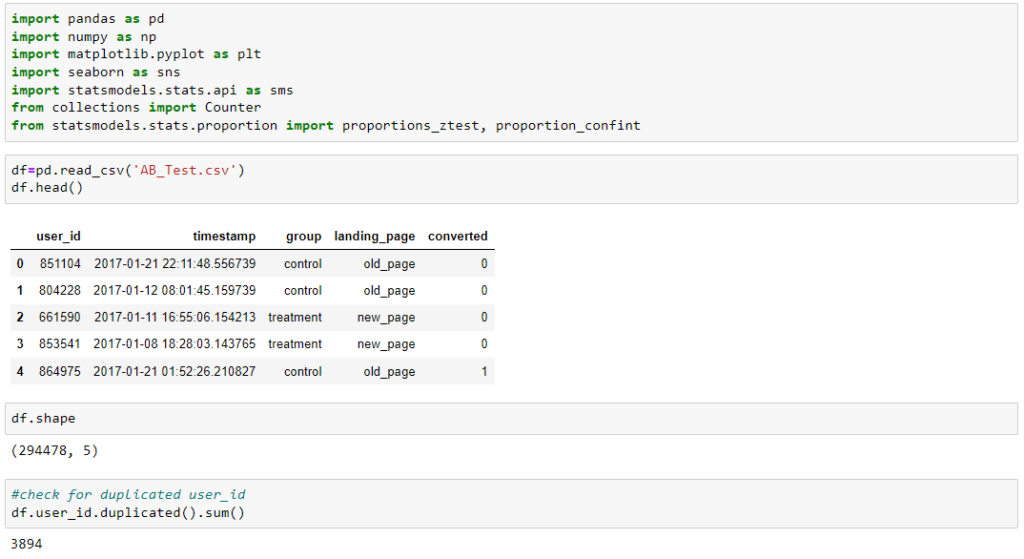
We have 3894 users that appear more than once. Since the number is pretty low we can remove all instances of double user_id to avoid sampling the same users twice.
drop_duplicates method can be used to get the unique user_id in the DataFrame
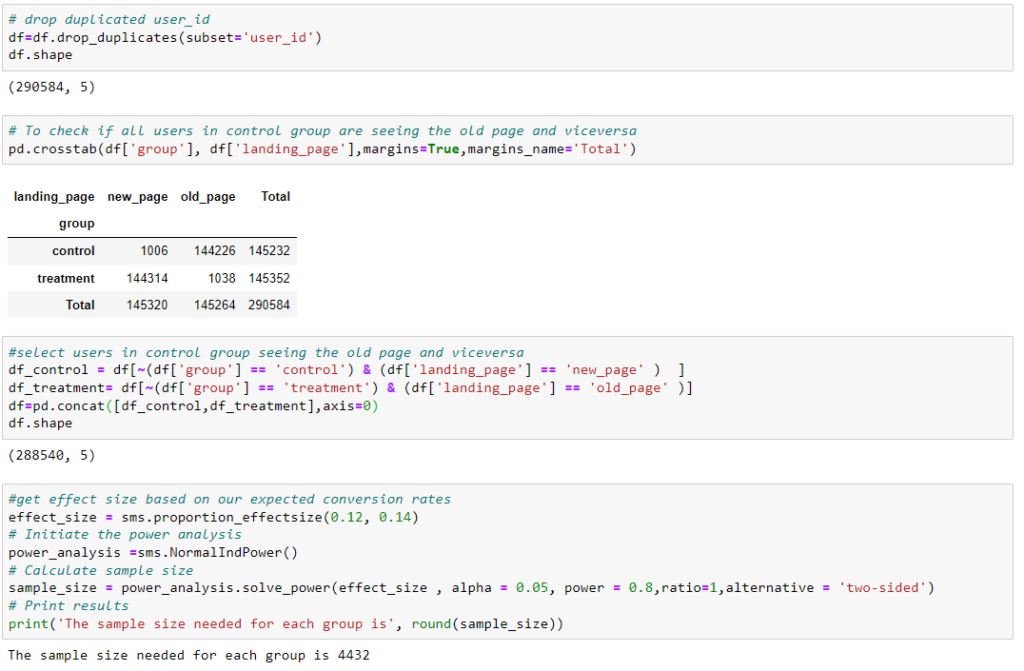
the suggested minimum number of samples in each group required is 4432 to have a significant p-value in the z-test. The power ratio = 1 means the number of samples in the control and treatment groups are the same.
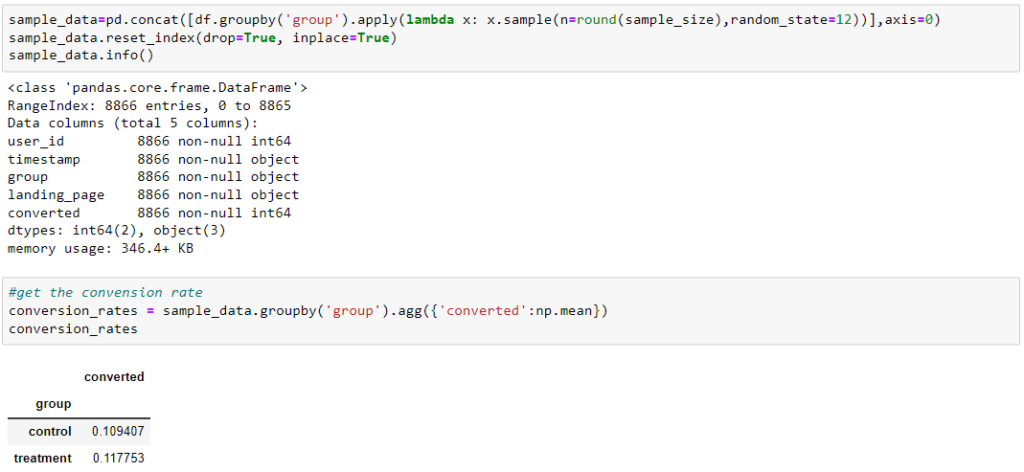
Has our design improved slightly ?
To answer the question let us test the hypothesis to see if this difference is statistically significant. Since our sample size is large we can assume that the underlying distribution is normal and z-test can be used.

P-value=0.216 is greater than the significance level (0.05). Consequently, we fail to reject null hypothesis. It indicates that our new design do not significantly outperform the old design.
